(2024/01/08 created) This page is on a Nonlinear Representative Theory proposed by Liang Zhao, Akiko Tanimoto, and Wenruo Lyu since late 2023.

(New) (2024/03/04) 非線形代表理論の日本語資料

Introduction

Q1: Given a group of people, how many representatives do we need for that group?

This question is important as it formulates one of the fundamental issue regarding the parliament, a core governmental institute that directly or indirectly affects everyone's life. A parliament consists of representatives of the people (the so-called indirect democracy). Therefore, a parliament should be large enough to represent the whole people. On the other hand, a fat parliament is not preferred, not only because it takes a huge amount of money to support this system (e.g., the annual expense for a member of the Japanese parliament is estimated to 150 million Yen, where the average income of Japanese is about 4 million Yen), but also because a fat parliament is more difficult to make efficient decision. Therefore, it is obvious that finding an appropriate size for a parliament is important.

Another fundamental issue regarding the parliament is the next.

Q2: Given the number of seats in a parliament, how should we apportion them to the subgroups?

This question challenges human wisdom for more than two centuries, even before the birth of the U.S. The point here is how to apportion seats with equality. In the old age, the apportionment did not consider the people belonging to some lower classes (thus they were not represented in the parliament). After a long history's fight and movement toward equality, today we have accepted a so-called proportional representation (PR) theory that counts everyone in the population and asks to apportion the seats proportionally to the population of the subgroups.

PR is a remarkable achievement of the human society, comparing to the old age when some people were not represented at all. Unfortunately, it uses a wrong formula in calculating the weight (contribution) of an individual. Speaking more precisely, the formula used by PR to calculate the weight of an individual is "#seats / population," which implicitly assumes that the size of a parliament is proportional to the population (Zhao, Tanimoto, Lyu, 2022). This implies that PR can only apportion the seats correctly (with equal weight) under very limited situation.

To address these two issues, we have developed a novel Nonlinear Representative Theory and here is a web page to explain this theory. This theory upgrades PR to a correct theory by explicitly introducing a standard function on an appropriate size of a parliament. We have published some articles regarding to this theory and are preparing more articles for publication.

Assumptions

The core assumptions of the NRT are the next two.

Assumption 1 There exists an appropriate number for representatives of a group of people and that number is not proportional to the population in general.

Assumption 2 If an appropriate number of representatives for a group of people is nonlinear to the population, the apportionment of seats to its subgroups shall also be nonlinear in order to achieve (individual) equality. PR is a special case when the appropriate number of representatives is (always) proportional (i.e.. linear) to the population.

Both assumptions contradict to (in fact, upgrades) the mainstream understanding on the aforementioned issues Q1 and Q2. We call it an upgrade of the existing literature because the existing theory can be viewed as a special case with a linear standard function. We will explain the detail in the following.

Why and how

For studying the first assumption, let us suppose that, after more than two centuries’ trial-and-error, human society has learned how to decide an appropriate size of a parliament from the population. Therefore, the practice and the real data shall tell us the appropriate size of a parliament. Have a look on the next figure please.

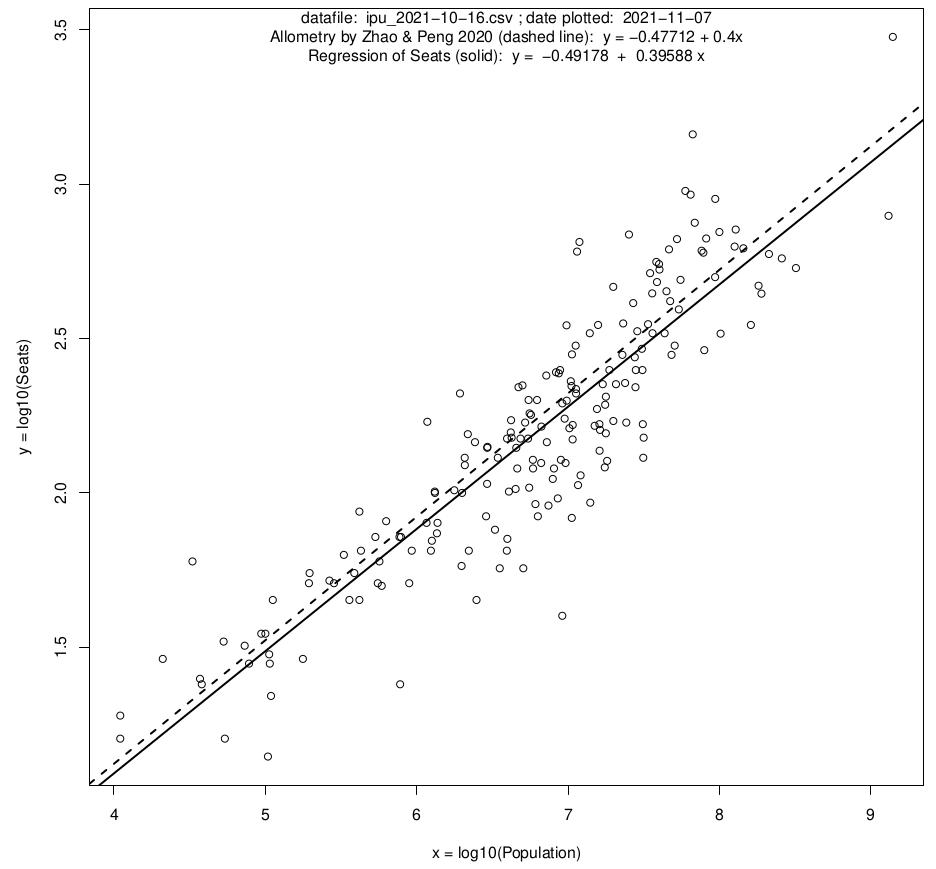
This figure plots, in log-log scale, the population and the size of parliament for all the 192 (out of about 200) countries that we could find the data (data source: IPU, 2021. The total number is used for bicameral countries.). It clearly shows that the size of a parliament is roughly proportional to the 0.4-th power of the population (Adjusted R2 = 0.80). In fact, there are a large amount of papers showing this fact for the half a century including two pioneering works R. Taagepera, 1972 and G.J. Stigler 1976. We remark that Taagepera was later awarded the Johan Skytte Prize in Political Science (the Nobel Prize for Political Science) in 2008, and Stigler was a Novel Laureates in Economic Sciences in 1982.

Theoretical models for the size of parliament has even longer history. The earliest work seems to be L. Penrose, 1946, who proposed a square root law, i.e., the size of a parliament shall be proportional to the square root of the population. We remark that Penrose is the father of R. Penrose, a Nobel Laureate in Physics in 2020. Taagepera, 1972 also proposed a model which is called the cube root law since it argues that the size of a parliament shall be proportional to the cube root of the population (recently Margaritondo claimed to have found a flaw in Taagepera, 1972 and revised it to a square root law). For a survey, see our paper Zhao et al. 2022.

There are a lot of models to explain the phenomenon. We are happy to contribute a social network-based theory. The latest publication: Zhao & Peng, An Allometric Scaling for the Number of Representative Nodes in Social Networks (a draft version is available on researchgate).

Summarizing the above, we consider Assumption 1 is rather obvious.

For the second assumption, this requires a deeper understanding on the weight (or contribution) of an individual to the number of seats. We will upload more content later. See our paper Zhao et al. 2022.

Publications

1. How to estimate the order of the number of representative nodes in a social network: Liang Zhao, Tianyi Peng. 2020. "An Allometric Scaling for the Number of Representative Nodes in Social Networks." In: Masuda, N., Goh, KI., Jia, T., Yamanoi, J., Sayama, H. (eds) Proceedings of NetSci-X 2020: Sixth International Winter School and Conference on Network Science. NetSci-X 2020. Springer Proceedings in Complexity. Springer, Cham. https://doi.org/10.1007/978-3-030-38965-9_4
2. On an appropriate size of a parliament (In Japanese): 趙亮，谷本明子，呂文若．2022．"最も好都合な議員定数"（第６章），「選挙・投票・公共選択の数理」，日本応用数理学会 監修・ 大山 達雄 編，共立出版 https://www.kyoritsu-pub.co.jp/book/b10011785.html
3. How to correctly calculate the (nonlinear) weight of an individual: Liang Zhao, Akiko Tanimoto, and Wenruo Lyu. 2022. "Standardizing Representation for Equality with a Population Seat Index" arxiv, https://arxiv.org/abs/2212.14790
4. Nonlinear representatives in subnational legislatures: Tanimoto, Akiko; Zhao, Liang, 2023, "Subnational Legislatures", https://doi.org/10.7910/DVN/A3QGLL, Harvard Dataverse, V3, UNF:6:1nucS7sjomZIZjs7D72+Rw== [fileUNF]
5. Rounding algorithms for the NRT (how to find whole number apportionment satisfying good properties): Lyu, Wenruo, and Liang Zhao. 2023. "Axioms and Divisor Methods for a Generalized Apportionment Problem with Relative Equality" Mathematics 11, no. 15: 3270. https://doi.org/10.3390/math11153270
6. Nonlinear Representative Theory (In Japanese): 趙亮，谷本明子，呂文若．2024．"非線形代表理論"，日本応用数理学会第20回研究部会連合発表会， 2024年3月4日～3月6日，長岡技術科学大学． 非線形代表理論の日本語資料